例えば、サイトの「今すぐ購入」ボタンの色の実験をしたいとします。現在、青（コントロールになる）ですが、緑（バリアント#1）と紫（バリアント#2）もテストしたいと考えています。個々の仮説検定の偽陽性の率が0.05（5％）である場合、帰無仮説がtrueであるときに統計的に有意な結果となる確率は次のとおりです。

1 - 0.95^2 = 0.0975

（これは、検定が独立していることを前提としています。）

言い換えれば、十分なテストを実行すれば、どのような場合も統計的に有意な結果を得ることができます。0.05の偽陽性の確率では、20件の仮説検定中に1件は、無作為の偶然だけで統計的に有意であると予想できます。

多重仮説の補正によって問われるのは、「この統計は偶然によるものか、それとも正しいか？」です。

偽陽性

偽陽性率という考えはご存知かもしれません。これは、次の比率です：

間違って陽性として記述された負のイベントの数と
実際の負のイベントの合計との比率。

すべての実験には、結果が偽陽性となるリスクがあります。これは、実際にはバリエーション間に実質的な差異がないのに、実験がどちらかの方向性があるとの結果を報告した場合に発生します。

偽陽性結果のリスクは、実験に指標またはバリアントを追加するごとに増加します。個々の指標またはバリアントでは偽陽性率が同じであるにもかかわらず、このことが当てはまります。

幸いなことに、多重比較問題を補正する統計ツールがあります。Amplitudeでは、ボンフェローニ補正を使います。

ボンフェローニ補正

ボンフェローニ補正は、多重比較問題に対処する最も単純な統計的手法です。また、より保守的な方法の1つであり、他の手法よりも偽陰性リスクが高くなります。例えば、ボンフェローニ補正は、すべての比較におけるp値の分布を考慮しません。すべての仮説で帰無仮説が真である場合、p値は一様であるとみなします。

ただし、ボンフェローニ補正は、1つでも偽陽性が現れる確率をコントロールし、信頼区間に適用します。上記のボタンの色の例では、0.1を2で割ると0.05であるため、探していたものとなります。したがって、1つでも偽陽性が現れる確率（少なくとも1つの仮説を棄却する確率）は制御されます。

**注：**証明は、ブールの不等式に従います。

数学的には、ボンフェローニ補正は偽陽性率を仮説検定の数で割り求めます。これは、p値に仮説検定の数を乗じたものと同じです。

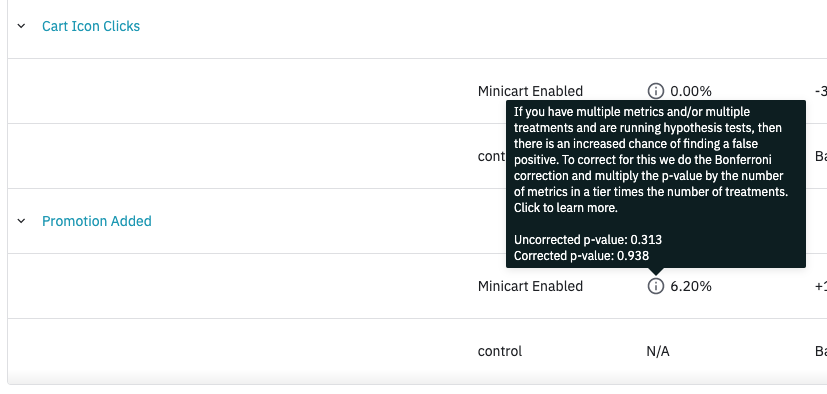
Amplitude Experimentは、2つの指標層（一次と二次）の各々の処置の数と指標の数の両方で、ボンフェローニ補正を行います。言い換えれば、ボンフェローニ補正は複数の処置（すなわち、2つ以上の処置）がある場合にのみ、主要指標に適用されます。複数の二次指標または複数の処置がある場合、ボンフェローニ補正は二次指標に適用されます。どちらの場合も、ボンフェローニ補正が適用されると、有意差の列に情報アイコンが表示されます。ツールチップは、補正済みおよび未補正のp値を表示します。

Need help? Contact Support

Visit Amplitude.com

Have a look at the Amplitude Blog

Learn more at Amplitude Academy