プライマリ指標モジュールで、+ Add Metricをクリックし、数式ドロップダウンオプションから数式を選択します。
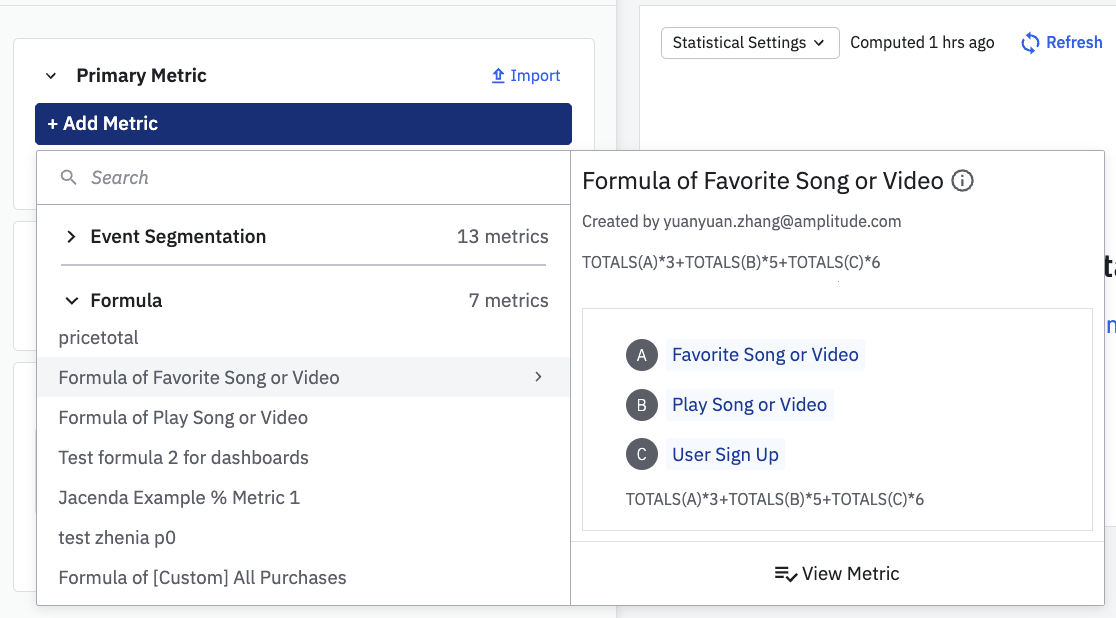
+ Define single-use metricをクリックし、表示されるモーダルで、指標タイプドロップダウンから数式を選択します。
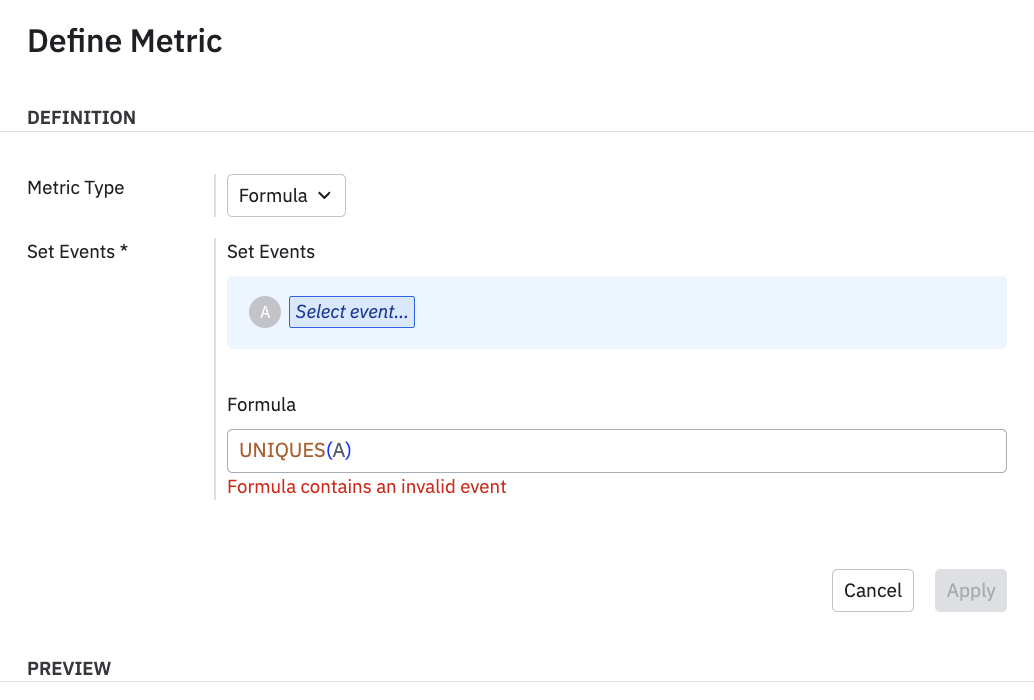
- イベント...を選択をクリックして、数式指標に含めるイベントの選択を開始する。すべてのイベントが含まれるまで、このステップを繰り返します。
- 数式ボックスで、数式指標を計算する数式を入力します。実験結果でサポートされている数式のリストについては、ここをクリックするか、数式構文の説明については、ここをクリックしてください。
- この新しい数式指標に名前を追加します。完了したら、適用をクリックします。指標は、実験結果チャートに追加されます。

オブジェクト管理センターでこの指標を表示することもできます。

サポートされている数式関数

次の数式関数は、実験結果でサポートされています。

UNIQUES:

構文：UNIQUES（イベント）

イベントをトリガーしたユニークユーザーの数を返します。

TOTALS：

構文：TOTALS（イベント）

イベントがトリガーされた時間の合計数を返します。

PROPSUM：

構文：PROPSUM（イベント）

この関数は、イベントの数値プロパティでグループ化されている場合のみ機能します。複数のプロパティでグループ化する場合、数式は、最初のグループバイクローズで計算を実行します。

指定されたイベントをグループ化しているプロパティ値の合計を返します。

PROPAVG：

構文：PROPAVG（イベント）

グループ化しているプロパティ値の平均を返します。この関数は、PROPSUM（イベント）/ TOTALS（イベント）と同じです。この記事では、AmplitudeがPROPAVGとPROPSUMをどのように計算するかについて、さらに詳しく学んでください

数式構文

数式で、イベントモジュールで対応する文字で選択したイベントを参照します。関数とパラメータは大文字小文字を区別しません。次の算術演算を実行することもできます。

数式指標で実験データが計算される方法を理解する前に、実験分析ビュー全体を理解することが重要です。

数式指標では、Amplitudeは、各関数の結果を独立して計算し、各関数の平均と分散を示します。算術演算子は、これらの個々の関数の結果に適用されます。

数式指標をTOTALS（A）+ TOTALS（B）として定義したと仮定します。 Amplitudeは、この指標の両方のコンポーネント、および共分散の分散と平均を計算します。

XをTOTALS（A）に、YをTOTALS（B）に等しいに設定すると、これに続くステートメントは次のとおりです。

V[X] =Xの分散
E[X] = Xの平均
V[Y] = Yの分散
E[Y] = Yの平均
Cov[X、Y] = XとYの共分散、すべての数学演算でゼロに仮定します。
**加算：**分散：V[X + Y] =nV[X] + nV[Y]
Mean：E[X + Y] =E[X] + E[Y]
減算：分散：V[X -Y] = nV[X] + nV[Y]Mean：E[X - Y] = E[X] - E[Y]
乗算：分散：V[X \*Y] = n^3 mu\_y^2 sigma\_x^2 + n^3 sigma\_y^2 mu\_x^2 + n^2 sigma\_x^2 sigma\_y^2Mean：E[X \* Y] = E[X] \* E[Y]
除算：分散：平均：E[X/ Y] =**![](/docs/output/img/jp/tbgmtKNhsfKgbfoHYYnWTI9Ib6GuGFwmXbRV1VHqr61oqN1PKYTufOTu5IQrTA9UwaC1U1P2Dvxf99ByeYe1EX9Ev0DlhpbwE-rCAzfUiPuksitYBYjB-kYr79VPfYT3_aYa66DYQdG4gMwg74h339w)** E[X] / E[Y]

全体的な数式指標の平均と分散が得られたら、信頼区間チャートとp値を計算できます。

数式/指標：TOTALS（A）/ TOTALS（B）

Have a look at the Amplitude Blog