The cumulative exposures graph: Increasing and decreasing slopes

The cumulative exposures graph details the number of users who are exposed to your experiment over time. The x-axis displays the date when the user was first exposed to your experiment; the y-axis displays a cumulative, running total of the number of users exposed to the experiment. 

Each user is only counted once, unless they are exposed to more than one experiment variant; in that case, they are counted once for each variant they see.

Interpreting the cumulative exposure graph

This article will discuss cumulative exposure results with:

• Increasing slope (the lines consistently go up and to the right)
• Decreasing slope (the lines go up and to the right, but the cumulative exposure slows down over time)

Be sure to check out other help center articles on interpreting cumulative exposure results with: 

• An inflection point or a flattened slope
• Divergent lines (similar or different slopes)

Increasing slope

In the graph below, each line represents a single variant. March 20 is the first day of the experiment, with 158 users triggering the exposure event for the control variant. A day later, a total of 314 users have been exposed to the control variant. That number is the sum of exposures on March 20 and March 21.

This is a very standard cumulative exposure graph with an increasing slope. 

Mathematically speaking, the slope of each line is the change in the y-axis divided by the change in the x-axis: 

1∆y / ∆x = (cumulative users exposed as of day T1 — cumulative users exposed as of day T0) / (number of days elapsed between T0 and T1) = Number of new users exposed to the experiment, per day, from day T0 to day T1.

What are some other things we can say about this graph?

• It’s cumulative, which means the y-axis will not decrease. The slope of the line is the number of new users exposed to your experiment every day. The line may slow down, or even stop growing completely. But you won’t see a cumulative exposures graph where the line peaks and then drops.
• There’s a dotted line at the end, which means there is incomplete data for those dates. See this article for more information.
• The two lines do not track each other perfectly. That’s because each line represents a unique variant, and exposures can differ slightly between variants, even when they’re set to receive the same amount of traffic.
• Both variants are on a steady growth path. This means there is no seasonality. If, for example, users were more likely to engage with your product (and therefore more likely to be exposed to an experiment) on weekdays, you’d see this in the chart: on weekends, the y-axis value would increase more slowly.

Hourly versus daily setting

Often, changing the x-axis to an hourly setting, as opposed to daily, will offer new ways of understanding your chart:

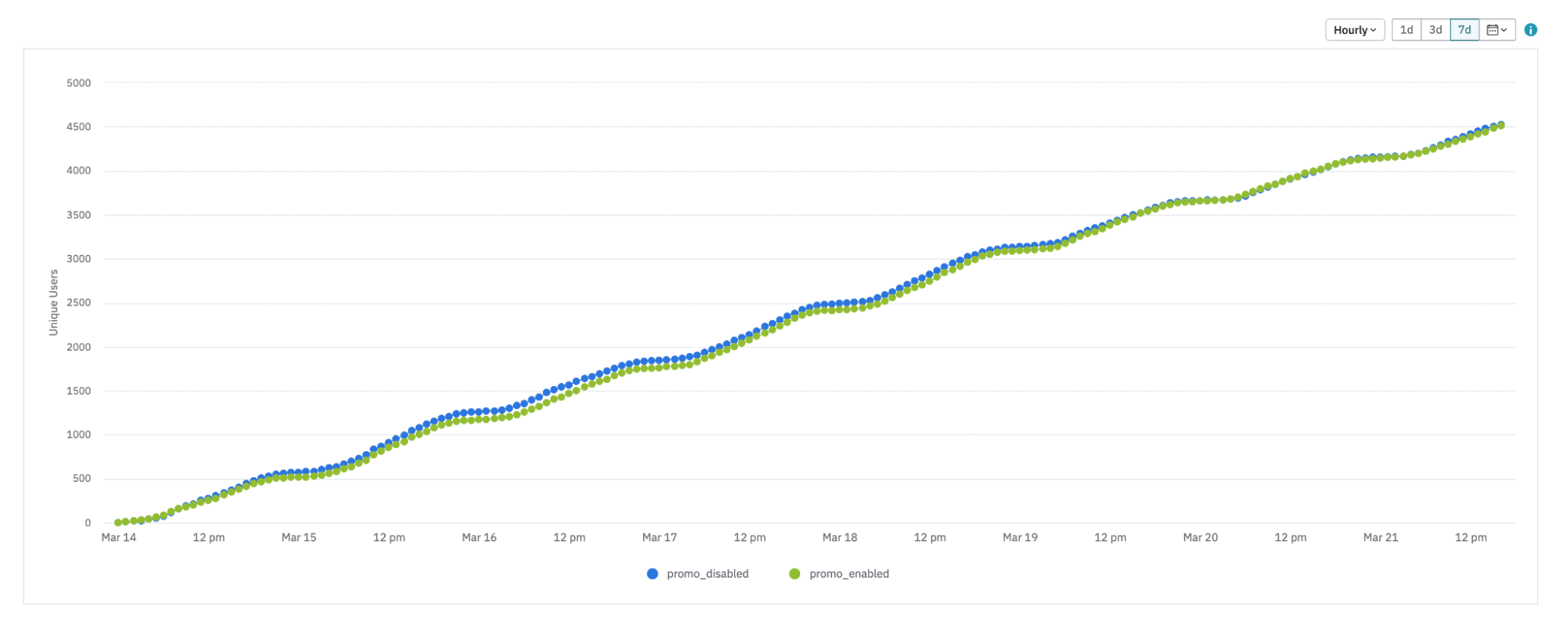
Here, the trend is still fairly linear. But since we are now looking at an hourly graph, we can see that from 9 pm to about 5 am, almost no additional users are being exposed to the experiment. This is probably when people are sleeping, so it stands to reason they are not using the product. This is something we couldn’t have seen in the daily version of the graph. 

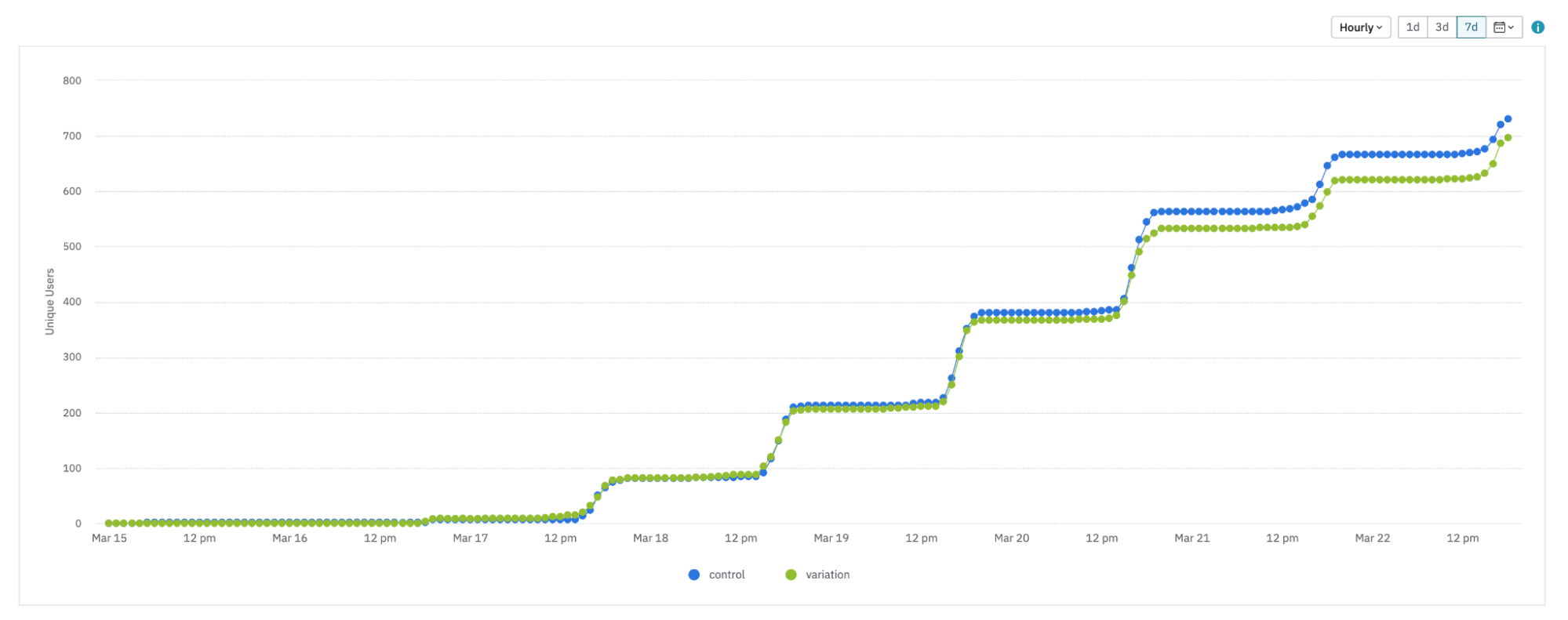
This is a more extreme example. Here, the exposures look like a step function. In this case, it could be that the users who have already been exposed to your experiment at least once are evaluating the feature flag again during these “flat” time periods. 

Decreasing slope

Sometimes, an experiment’s cumulative exposures can start out strong but then slow down over time.

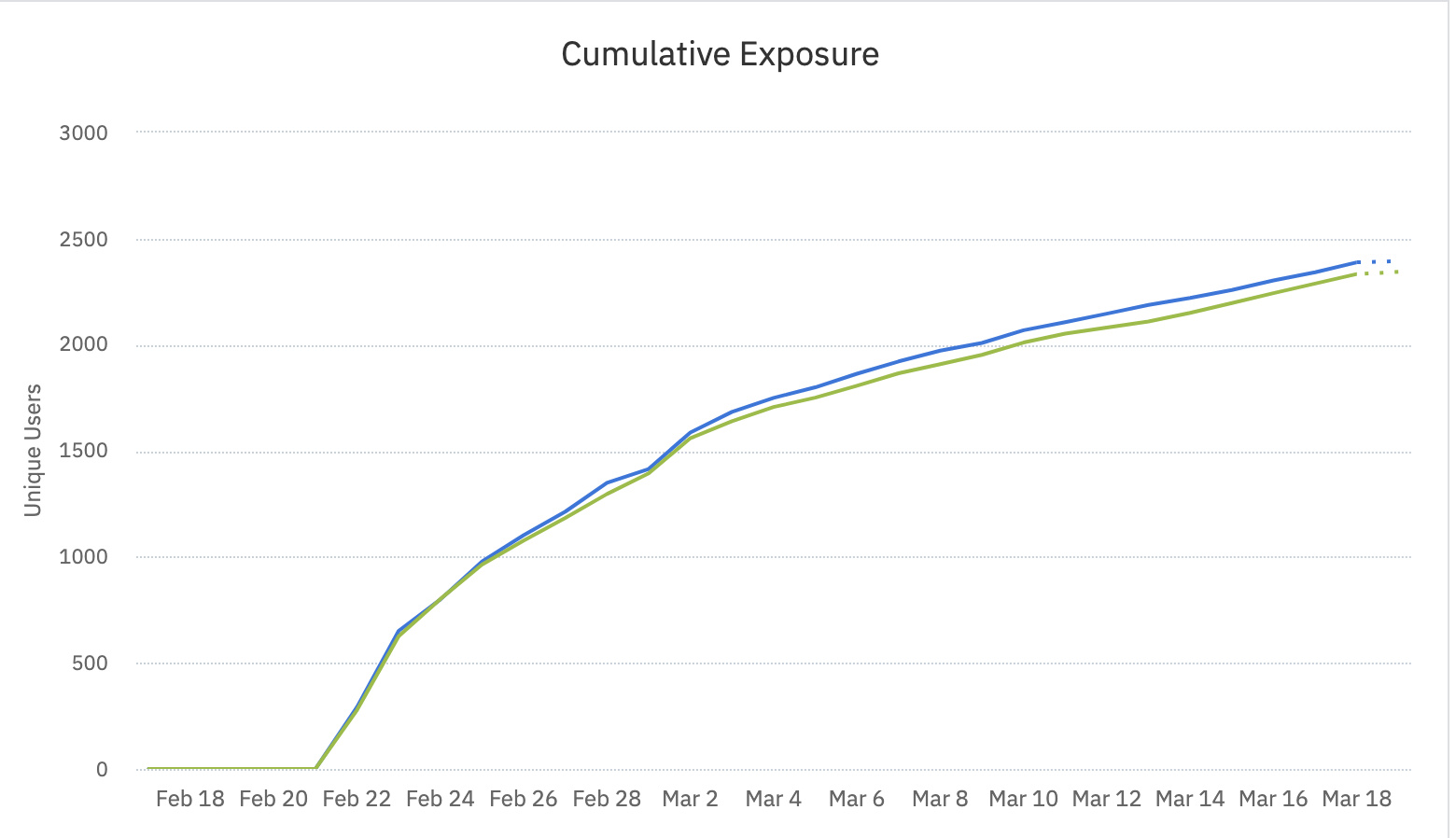
When this experiment launched, each variant was exposed to about 280 new users each day. But toward the end, those exposure rates were down to about 40 new users per variant, per day.

Static cohorts can limit your experiment

The cumulative exposures can flatten out over time when you’re targeting a static cohort—i.e., one that does not grow or shrink on its own.

For example, imagine a static cohort with 100 members. On the first day, your experiment was shown to 40 of those users. That leaves only 60 more users eligible to be included in the future. With each passing day, there are fewer and fewer users who can enter into the experiment in the first place, and the slope of your cumulative exposures graph will inevitably flatten. 

If you’re using a static cohort in an experiment, consider rethinking how you’re using the duration estimator. Instead of solving for the sample size, you should ask what level of lift you can reasonably detect with this fixed sample size. 

Whenever you use a cohort in this way, ask yourself whether the cohort is actually representative of a larger population that would show a similar lift if more users were exposed to the winning variant. You can’t assume this; doing so would be like running an experiment in one country and then assuming you’ll see the same impact in any other country. 

Other possible causes for decreasing slope

• Using a dynamic cohort that isn’t growing quickly enough, or the number of users that interact with your experiment might be limited.
• How you handle sticky bucketing: If users enter the cohort and then exit, do you want them to continue to see the experiment (for consistency’s sake) even though they no longer meet the targeting criteria?
• The experiment is initially shown to a group of users who are not representative of users exposed later. Users who have been using your product for 30 days may interact with the feature you’re testing differently than those who’ve been around for 100 days, for example. Consider running your experiment for longer than you had originally planned, to make sure you’re studying the effect of the treatment on a steady state of users.
• Users gradually become numb to your experiment and stop responding to it after repeated exposures.

Bear in mind that just because the cumulative exposures graph has flattened out does not mean that the experiment has a limited impact. It all depends on the specifics of your users’ behavior.

Seeing this kind of graph has serious implications regarding how long you will need to run your experiment. The standard method of calculating the duration of an experiment is to use a sample size calculator and divide the estimated number of samples by the average traffic per day. Here, that’s not the case. Generally, you’ll need to run the experiment for longer than expected, since the denominator was overestimated.